PROGRESSÕES
PROGRESSÃO ARITMÉTICA - P.A.
Definição
É uma sequência em que cada termo, a partir do segundo. É a soma do anterior com uma constante, denominada razão. Esta razão e representada pela letra r.
Elementos
a1 : 1o termo
an : termo genérico, termo geral (ou n-ésimo termo)
r : razão
n : número de termos
Sn : soma dos termos
TM : termo médio
Fórmula do termo Geral da P.A.
an = a1 + (n-1).r
Interpolação Aritmética
Interpolar ou inserir 'k' meios aritméticos entre os termos a1 e an significa formar uma progressão aritmética de 'k + 2' termos, onde a1 e an são extremos.
Soma dos Termos da P.A.
A soma dos termos de uma P.A. limitada (ou finita) é igual ao produto da semi soma dos extremos pelo número de termos.
Termo Médio de uma P.A.
Consequência da Fórmula da Soma
P.A. de número ÍMPAR de termos Sn = TM .
Si - Sp = TM
onde:
Si = a1 + a3+ a5 + ... e Sp = a2+ a4 + a6 + ...
P.A. de número PAR de termos:
Representação de 3 termos na P.A.
Quando três termos desconhecidos estão em progressão aritmética, pode-se usar o seguinte artifício:
(x-r) ; x ; (x+r)
Exercícios - Progressão Aritmética - P.A.
Questões de P.A.
1-) Encontre o termo geral da P.A. (2, 7, ...).
2-) Encontre o termo geral da P.A. (7/3, 11/4, ...).
3-) Qual é o décimo quinto termo da P.A. (4, 10, ...).
4-) Qual é o centésimo número natural par ?
5-) Ache 0 5º termo da P.A. (a+b ; 3a-2b ; ...).
6-) Ache o sexagésimo número natural ímpar.
7-) Numa P.A. de razão 5, o primeiro termo é 4. Qual é a posição do termo igual a 44 ?
8-) Ache a1 numa P.A., sabendo que r=1/4 e a17=21.
9-) Quantos termos tem uma P.A. finita, de razão 3, sabendo-se que o primeiro termo é -5 e o último é 16 ?
10-) Calcule o número de termos da P.A. (5, 10, ..., 785).
11-) Qual é o primeiro termo de uma P.A. cujo sétimo termo é 46, sendo o termo precedente 39 ?
12-) Quantos múltiplos de 7 podemos escrever com 3 algarismos ?
13-) Quantos são os números naturais menores que 98 e divisíveis por 5 ?
14-) Quantos números inteiros existem, de 100 a 500, que não são divisíveis por 8 ?
15-) Interpole 11 meios aritméticos entre 1 e 37.
16-) Quantos termos aritméticos devemos interpolar entre 2 e 66 para que a razão da interpolação seja 8 ?
17-) Determine a média aritmética dos seis meios aritméticos que podem ser interpolados entre 10 e 500.
18-) Numa estrada existem dois telefones instalados no acostamento: um no quilometro 3 e outro no quilometro 88. Entre eles serão colocados mais 16 telefones, mantendo-se entre dois telefones consecutivos sempre a mesma distância. Determine em quais marcos quilométricos deverão ficar esses novos telefones.
19-) (ITA-SP) Quantos números inteiros existem, de 1000 a 10000, que não são divisíveis nem por 5 nem por 7 ?
20-) Uma fábrica produziu, em 1986, 6530 unidades de um determinado produto e, em 1988, produziu 23330 unidades do mesmo produto. Sabendo que a produção anual desse produto vem crescendo em progressão aritmética, pede-se:
a) Quantas unidades do produto essa fábrica produziu em 1987 ?
b) Quantas unidades foram produzidas em 1991 ?
Respostas das questões de P.A.
Questão 1
Dados: a1 = 2 ; r = 7 - 2 = 5 ; an = ? ; n = ?
Resolução:
an = a1 + (n-1).r
an = 2 + (n -1).5
an = 2 + 5n - 5
an= 5n - 3
Resposta: an = 5n - 3
Questão 2
Dados: a1= 7/3 ; r = 11/4 - 7/3 = (33 - 28)/12 = 5/12 ; an = ? ; n = ?
Resolução:
an = a1 + (n-1).r
an= 7/3 + (n -1). 5/12
an = 7/3 + 5/12n - 5/12
an= 5/12n + 28/12 - 5/12
an = 5/12n + 23/12
Resposta: an= 5/12n + 23/12 ou an = (5n + 23)/12
Questão 3
Dados: a1 = 4 ; r = 10 - 4 = 6 ; an= a15 = ? ; n = 15
Resolução:
an = a1 + (n-1).r
a15 = 4 + (15 -1).6
a15= 4 + 14.6
a15 = 4 + 84
a15= 88
Resposta: a15 = 88
Questão 4
Dados: a1 = 0 ; r = 2 - 0 = 2 ; an = a100= ? ; n = 100
Resolução:
an = a1 + (n-1).r
a100 = 0 + (100 -1).2
a100 = 0 + 99.2
a100= 198
Resposta: a100 = 198
Questão 5
Dados: a1 = a+b
r = (3a-2b)-(a+b)
r = 3a-2b - a-b
r = 2a-3b
an = a5= ? ; n = 5
Resolução:
an= a1+ (n-1).r
a5= a+b + (5-1).(2a-3b)
a5 = a+b + 4.(2a-3b)
a5= a+b +8a-12b
a5 = 9a - 11b
Resposta: a5= 9a - 11b
Questão 6
Dados: a1 = 1 ; r = 3 - 1 = 2 ; an = a60= ? ; n = 60
Resolução:
an = a1 + (n-1).r
a60 = 1 + (60 -1).2
a60 = 1 + 59.2
a60 = 1 + 118
a60 = 119
Resposta: a60 = 119
Questão 7
Dados: a1 = 4 ; r = 5 ; an = 44 ; n = ?
Resolução:
an = a1 + (n-1).r
44 = 4 + (n-1).5
44 = 4 + 5n -5
44 -4 + 5 = 5n
45 = 5n
45/5 = n
9 = n ou n = 9
Resposta: 9ª posição
Questão 8
Dados: a1 = ? ; r = 1/4 ; a17 = 21 ; n = 17
Resolução:
an = a1 + (n-1).r
a17 = a1 + (17-1).(1/4)
21 = a1 + 16/4
21 = a1 + 4
21 - 4 = a1
17 = a1
Resposta: a1 = 17
Questão 9
Dados: a1 = -5 ; r = 3 ; an = 16 ; n = ?
Resolução:
an = a1 + (n-1).r
16 = -5 + (n-1).3
16 = -5 + 3n -3
16 = 3n - 8
16 + 8 = 3n
24 = 3n
24/3 = n
8 = n
Resposta: n = 8
Questão 10
Dados: a1 = 5 ; r = 5 ; an = 785 ; n = ?
Resolução:
an = a1 + (n-1).r
785 = 5 + (n-1).5
785 = 5 + 5n -5
785 = 5n
785/5 = n
157 = n
Resposta: n = 157
Questão 11
Dados: a1 = ? ; an = a7 = 46 ; a6 = 39 ; r = a7 - a6 ; r = 46 - 39 ==> r = 7 ; n = 7
Resolução:
an = a1 + (n-1).r
46 = a1 + (7-1).7
46 = a1 + 6.7
46 = a1 + 42
46 - 42 = a1
4 = a1
Resposta: a1 = 4
Questão 12
Dados: P.A.(105,...,994); a1 = 105 ; an = 994 ; r = 7 ; n = ?
Resolução:
an = a1 + (n-1).r
994 = 105 + (n-1).7
994 = 105 + 7n - 7
994 = 105 - 7 + 7n
994 = 98 + 7n
994 - 98 = 7n
896 = 7n
896/7 = n
128 = n
Resposta: n = 128
Questão 13
Dados: P.A.(0,...,95); a1 = 0 ; an = 95 ; r = 5 ; n = ?
Resolução:
an = a1 + (n-1).r
95 = 0 + (n-1).5
95 = 0 + 5n - 5
95 + 5 = 5n
100 = 5n
100 = 5n
100/5 = n
20 = n
Resposta: n = 20
Questão 14
1-) Calculamos a quantidade de números, entre 100 e 500, que são divisíveis por 8.
Dados: P.A.(104,...,496); a1 = 104 ; an = 496 ; r = 8 ; n = ?
Resolução:
an = a1 + (n-1).r
496 = 104 + (n-1).8
496 = 104 + 8n - 8
496 = 96 + 8n
496 - 96 = 8n
400 = 8n
400/8 = n
50 = n
2-) Calculamos a quantidade de todos os números, entre 100 e 500.
Dados: P.A.(100,...,500); a1 = 100 ; an = 500 ; r = 1 ; n = ?
Resolução:
an = a1 + (n-1).r
500 = 100 + (n-1).1
500 = 100 + n - 1
500 = 99 + n
500 - 99 = n
401 = n
3-) Calculamos o número de termos que não são divisíveis por 8, fazendo: n = 401 - 50 = 351
Resposta: n = 351
Questão 15
P.A.(1, _, _, _, _, _, _, _, _, _, _, _,37)
Dados: a1 = 1 ; r = ? ; an = a13 = 37 ; n = 13
Resolução:
an = a1 + (n-1).r
a13 = 1 + (13-1).r
37 = 1 + 12.r
37 -1 = 12r
36 = 12r
36/12 = r
3 = r
Calculamos as 11 interpolações:
a2 = a1 + r = 1+3 = 4
a3 = a2 + r = 4+3 = 7
a4 = a3 + r = 7+3 = 10
a5 = a4 + r = 10+3 = 13
a6 = a5 + r = 13+3 = 16
a7 = a6 + r = 16+3 = 19
a8 = a7 + r = 19+3 = 22
a9 = a8 + r = 22+3 = 25
a10 = a9 + r = 25+3 = 28
a11 = a10 + r = 28+3 = 31
a12 = a11 + r = 31+3 = 34
Resposta: P.A.(1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37)
Questão 16
Dados: P.A.(2,...,66); a1 = 2 ; an = 66 ; r = 8 ; n = ?
Resolução:
an = a1 + (n-1).r
66 = 2 + (n-1).8
66 = 2 + 8n - 8
66 = 8n - 6
66 + 6 = 8n
72 = 8n
72/8 = n
9 = n
Subtraímos 2 termos dos 9 termos encontrados: n = 9 - 2 = 7.
Resposta: n = 7
Questão 17
Dados: P.A.(10, _, _, _, _, _, _,500); a1 = 10 ; an = a8 = 500 ; r = ? ; n = 8
Resolução:
an = a1 + (n-1).r
500 = 10 + (8-1).r
500 = 10 + 7.r
500 - 10 = 7r
490 = 7r
490/7 = r
70 = r
Calculamos as 6 interpolações:
a2 = a1 + r = 10+70 = 80
a3 = a2 + r = 80+70 = 150
a4 = a3 + r = 150+70 = 220
a5 = a4 + r = 220+70 = 290
a6 = a5 + r = 290+70 = 360
a7 = a6 + r = 360+70 = 430
Calculamos a média aritmética:
M.A. = Adição dos termos / número de termos adicionados = (a2 + a3 + a4 + a5 + a6 + a7) / 6
M.A. = (80 + 150 + 220 + 290 + 360 + 430) / 6 = 1530 / 6 = 255
Resposta: M.A. = 255
Questão 18
P.A.(3,..,88)
Dados: a1 = 3 ; r = ? ; an = a18 = 88 ; n = 18
Resolução:
an = a1 + (n-1).r
a18 = 3 + (18-1).r
88 = 3 + 17.r
88 - 3 = 17r
85 = 17r
85/17 = r
5 = r
Calculamos as 16 interpolações:
a2= a1 + r = 3+5 = 8
a3= a2 + r = 8+5 = 13
a4= a3 + r = 13+5 = 18
a5= a4 + r = 18+5 = 23
a6= a5 + r = 23+5 = 28
a7= a6 + r = 28+5 = 33
a8= a7 + r = 33+5 = 38
a9= a8 + r = 38+5 = 43
a10= a9+ r = 43+5 = 48
a11= a10+ r = 48+5 = 53
a12= a11+ r = 53+5 = 58
a13= a12+ r = 58+5 = 63
a14= a13+ r = 63+5 = 68
a15= a14+ r = 63+5 = 73
a16= a15+ r = 73+5 = 78
a17= a16+ r = 78+5 = 83
Resposta: Marcos quilométricos: 8, 13, 18, 23, 28, 33, 38, 43, 48, 53, 58, 63, 68, 73, 78, 83
Questão 19
Dados:
M(5) = 1000, 1005, ..., 9995, 10000.
M(7) = 1001, 1008, ..., 9996.
M(35) = 1015, 1050, ... , 9975.
M(1) = 1, 2, ..., 10000.
Resolução:
Para múltiplos de 5, temos: an = a1+ (n-1).r => 10000 = 1000 + (n - 1). 5 => n = 9005 / 5 => n = 1801.
Para múltiplos de 7, temos: an = a1+ (n-1).r => 9996 = 1001 + (n - 1). 7 => n = 9002 / 7 => n = 1286.
Para múltiplos de 35, temos: an = a1 + (n - 1).r => 9975 = 1015 + (n - 1).35 => n = 8995 / 35 => n = 257.
Para múltiplos de 1, temos: an = a1 + (n -1).r => 10000 = 1000 + (n - 1).1 => n = 9001.
Sabemos que os múltiplos de 35 são múltiplos comuns de 5 e 7, isto é, eles aparecem no conjunto dos múltiplos de 5 e no conjunto dos múltiplos de 7 (daí adicionarmos uma vez tal conjunto de múltiplos).
Total = M(1) - M(5) - M(7) + M(35).
Total = 9001 - 1801 - 1286 + 257 = 6171
Resposta: n = 6171
Questão 20
P.A.(6530, _ , 23330)
Dados: a1 = 6530 ; r = ? ; an = 23330 ; n = 3
Resolução:
an = a1 + (n-1).r
a3 = 6530 + (3-1).r
23330 = 6530 + 2.r
23330 - 6530 = 2r
16800 = 2r
16800/2 = r
8400 = r
a2 = a1 + r
a2 = 6530 + 8400
a2 = 14930
P.A.(6530, 14930, 23330, _ , _, _)
Dados:
a1 = 6530 ; r = 8400 ; an = a6 = ? ; n = 6
Resolução:
an = a1 + (n-1).r
a6 = 6530 + (6-1).8400
a6 = 6530 + 5.8400
a6 = 6530 + 42000
a6 = 48530
Resposta: a) 14930; b) 48530
----------------------------------------------------------------------------------------------------
PROGRESSÃO GEOMÉTRICA - P.G.
Definição
É uma sequência em que cada termo, a partir do segundo, é o produto do anterior com uma constante, denominada razão, representada pela letra 'q'.
Elementos
a1 : 1o termo
an : termo genérico, termo geral (ou n-ésimo termo)
q : razão
n : número de termos
Sn : soma dos termos
Pn : produto dos termos
Fórmula do Termo Geral da P.G.
an = a1 . qn-1
Produtos dos Termos de uma P.G.
O produto dos 'n' termos de uma P.G. é dado por:
ou
Obs.: para -1 < q < 1 e o número de termos tendendo ao infinito.
Termo Médio de uma P.G.
TM2 = a1.an
Representação de 3 termos na P.G.
Para representar três termos em P.G., sendo dado o produto dos termos, use:
Exercícios - Progressão Geométrica - P.G.
Questões de P.G
1-) Escreva os cinco primeiros termos de cada P.G., sendo dados:
a) a1 = 2 e q = 3
Resposta: P.G. (2, 6, 18, 54, 162, ...)
b) a1 = 3 e q = -1
Resposta: P.G. (3, -3, 3, -3, 3, ...)
c) a1 = -6 e q = 1/2
Resposta: P.G. (-6; -3; -1,5; -0,75; -0,375; ...) ou (-6; -3; -3/2; -3/4; -3/8; ...)
d) a1 = -2 e q = 5/4
Resposta: P.G. (-2; -5/2; -25/8; -125/32; -625/128; ...)
e) a1 = 7 e q = 0
Resposta: P.G. (7, 0, 0, 0, 0, 0, ...)
f) a1 = q = 1
Resposta: P.G. (1, 1, 1, 1, 1, ...)
2-) Calcule o valor do primeiro termo de uma P.G., sabendo que o quarto termo é -108 e a razão é q = 3.
3-) A soma do 2º com o 3º termo de uma P.G. vale 16 e o produto do 1º com o 3º é 16. Determine essa P.G. sabendo que ela é crescente.
Resolução:
a2 + a3 = 16 (I)
a1 . a3 = 16 (II)
Fazer a3 = a1 . q2 e substituir em (II).
a1 . a1 . q2 = 16
a12 . q2 = 42
Extrair a raiz quadrada dos dois membros.
a1 . q = 4
a1 = 4/q
Se a2 = a1 .q
a2 = 4/q . q
a2 = 4
Como a2 + a3 = 16, temos:
a3 = 12
q = a3 / a2 = 12/4 = 3
Daí a1 = 4/q
a1 = 4/3
Resposta: P.G. (4/3, 4, 12, ...)
4-) Interpole quatro meios geométricos entre 1/8 e 4.
5-) Interpole seis meios geométricos entre 1 e 2187.
Resolução:
an = a1. qn-1
2187 = 1 . q8-1
2187 = 1 . q7
Fatorando 2187, temos: 2187 = 37.
Então, 37 = q7
Se os expoentes são iguais, as bases das potências também são iguais. Logo, q = 3
a2 = a1 . q
a3 = a2 . q
a4 = a3 . q
a5 = a4 . q
a6 = a5 . q
a7 = a6 . q
P.G.(1, 3, 9, 27, 81, 243, 729, 2187)
6-) Uma pessoa aplicou R$ 8.000,00 à taxa de 2,5 por cento ao mês. Calcule por quanto tempo esse dinheiro deve ficar aplicado para que o montante seja de R$ 11.586,38. (Use log 1,025 = 0,0107 e log 1,4129732 = 0,1501.)
7-) Calcule a soma dos 6 primeiros termos da P.G. (7, 14, ...).
Resolução:
Sn = a1. (qn - 1) / q - 1
S6 = 7 . (26 - 1) / 2 - 1
S6 = 7 . (64 - 1) / 1
S6 = 7 . 63
S6 = 441
r : razão
n : número de termos
Sn : soma dos termos
TM : termo médio
Fórmula do termo Geral da P.A.
an = a1 + (n-1).r
Interpolação Aritmética
Interpolar ou inserir 'k' meios aritméticos entre os termos a1 e an significa formar uma progressão aritmética de 'k + 2' termos, onde a1 e an são extremos.
Soma dos Termos da P.A.
A soma dos termos de uma P.A. limitada (ou finita) é igual ao produto da semi soma dos extremos pelo número de termos.
Termo Médio de uma P.A.
Consequência da Fórmula da Soma
P.A. de número ÍMPAR de termos Sn = TM .
Si - Sp = TM
onde:
Si = a1 + a3+ a5 + ... e Sp = a2+ a4 + a6 + ...
P.A. de número PAR de termos:
Representação de 3 termos na P.A.
Quando três termos desconhecidos estão em progressão aritmética, pode-se usar o seguinte artifício:
(x-r) ; x ; (x+r)
Exercícios - Progressão Aritmética - P.A.
Questões de P.A.
1-) Encontre o termo geral da P.A. (2, 7, ...).
2-) Encontre o termo geral da P.A. (7/3, 11/4, ...).
3-) Qual é o décimo quinto termo da P.A. (4, 10, ...).
4-) Qual é o centésimo número natural par ?
5-) Ache 0 5º termo da P.A. (a+b ; 3a-2b ; ...).
6-) Ache o sexagésimo número natural ímpar.
7-) Numa P.A. de razão 5, o primeiro termo é 4. Qual é a posição do termo igual a 44 ?
8-) Ache a1 numa P.A., sabendo que r=1/4 e a17=21.
9-) Quantos termos tem uma P.A. finita, de razão 3, sabendo-se que o primeiro termo é -5 e o último é 16 ?
10-) Calcule o número de termos da P.A. (5, 10, ..., 785).
11-) Qual é o primeiro termo de uma P.A. cujo sétimo termo é 46, sendo o termo precedente 39 ?
12-) Quantos múltiplos de 7 podemos escrever com 3 algarismos ?
13-) Quantos são os números naturais menores que 98 e divisíveis por 5 ?
14-) Quantos números inteiros existem, de 100 a 500, que não são divisíveis por 8 ?
15-) Interpole 11 meios aritméticos entre 1 e 37.
16-) Quantos termos aritméticos devemos interpolar entre 2 e 66 para que a razão da interpolação seja 8 ?
17-) Determine a média aritmética dos seis meios aritméticos que podem ser interpolados entre 10 e 500.
18-) Numa estrada existem dois telefones instalados no acostamento: um no quilometro 3 e outro no quilometro 88. Entre eles serão colocados mais 16 telefones, mantendo-se entre dois telefones consecutivos sempre a mesma distância. Determine em quais marcos quilométricos deverão ficar esses novos telefones.
19-) (ITA-SP) Quantos números inteiros existem, de 1000 a 10000, que não são divisíveis nem por 5 nem por 7 ?
20-) Uma fábrica produziu, em 1986, 6530 unidades de um determinado produto e, em 1988, produziu 23330 unidades do mesmo produto. Sabendo que a produção anual desse produto vem crescendo em progressão aritmética, pede-se:
a) Quantas unidades do produto essa fábrica produziu em 1987 ?
b) Quantas unidades foram produzidas em 1991 ?
Respostas das questões de P.A.
Questão 1
Dados: a1 = 2 ; r = 7 - 2 = 5 ; an = ? ; n = ?
Resolução:
an = a1 + (n-1).r
an = 2 + (n -1).5
an = 2 + 5n - 5
an= 5n - 3
Resposta: an = 5n - 3
Questão 2
Dados: a1= 7/3 ; r = 11/4 - 7/3 = (33 - 28)/12 = 5/12 ; an = ? ; n = ?
Resolução:
an = a1 + (n-1).r
an= 7/3 + (n -1). 5/12
an = 7/3 + 5/12n - 5/12
an= 5/12n + 28/12 - 5/12
an = 5/12n + 23/12
Resposta: an= 5/12n + 23/12 ou an = (5n + 23)/12
Questão 3
Dados: a1 = 4 ; r = 10 - 4 = 6 ; an= a15 = ? ; n = 15
Resolução:
an = a1 + (n-1).r
a15 = 4 + (15 -1).6
a15= 4 + 14.6
a15 = 4 + 84
a15= 88
Resposta: a15 = 88
Questão 4
Dados: a1 = 0 ; r = 2 - 0 = 2 ; an = a100= ? ; n = 100
Resolução:
an = a1 + (n-1).r
a100 = 0 + (100 -1).2
a100 = 0 + 99.2
a100= 198
Resposta: a100 = 198
Questão 5
Dados: a1 = a+b
r = (3a-2b)-(a+b)
r = 3a-2b - a-b
r = 2a-3b
an = a5= ? ; n = 5
Resolução:
an= a1+ (n-1).r
a5= a+b + (5-1).(2a-3b)
a5 = a+b + 4.(2a-3b)
a5= a+b +8a-12b
a5 = 9a - 11b
Resposta: a5= 9a - 11b
Questão 6
Dados: a1 = 1 ; r = 3 - 1 = 2 ; an = a60= ? ; n = 60
Resolução:
an = a1 + (n-1).r
a60 = 1 + (60 -1).2
a60 = 1 + 59.2
a60 = 1 + 118
a60 = 119
Resposta: a60 = 119
Questão 7
Dados: a1 = 4 ; r = 5 ; an = 44 ; n = ?
Resolução:
an = a1 + (n-1).r
44 = 4 + (n-1).5
44 = 4 + 5n -5
44 -4 + 5 = 5n
45 = 5n
45/5 = n
9 = n ou n = 9
Resposta: 9ª posição
Questão 8
Dados: a1 = ? ; r = 1/4 ; a17 = 21 ; n = 17
Resolução:
an = a1 + (n-1).r
a17 = a1 + (17-1).(1/4)
21 = a1 + 16/4
21 = a1 + 4
21 - 4 = a1
17 = a1
Resposta: a1 = 17
Questão 9
Dados: a1 = -5 ; r = 3 ; an = 16 ; n = ?
Resolução:
an = a1 + (n-1).r
16 = -5 + (n-1).3
16 = -5 + 3n -3
16 = 3n - 8
16 + 8 = 3n
24 = 3n
24/3 = n
8 = n
Resposta: n = 8
Questão 10
Dados: a1 = 5 ; r = 5 ; an = 785 ; n = ?
Resolução:
an = a1 + (n-1).r
785 = 5 + (n-1).5
785 = 5 + 5n -5
785 = 5n
785/5 = n
157 = n
Resposta: n = 157
Questão 11
Dados: a1 = ? ; an = a7 = 46 ; a6 = 39 ; r = a7 - a6 ; r = 46 - 39 ==> r = 7 ; n = 7
Resolução:
an = a1 + (n-1).r
46 = a1 + (7-1).7
46 = a1 + 6.7
46 = a1 + 42
46 - 42 = a1
4 = a1
Resposta: a1 = 4
Questão 12
Dados: P.A.(105,...,994); a1 = 105 ; an = 994 ; r = 7 ; n = ?
Resolução:
an = a1 + (n-1).r
994 = 105 + (n-1).7
994 = 105 + 7n - 7
994 = 105 - 7 + 7n
994 = 98 + 7n
994 - 98 = 7n
896 = 7n
896/7 = n
128 = n
Resposta: n = 128
Questão 13
Dados: P.A.(0,...,95); a1 = 0 ; an = 95 ; r = 5 ; n = ?
Resolução:
an = a1 + (n-1).r
95 = 0 + (n-1).5
95 = 0 + 5n - 5
95 + 5 = 5n
100 = 5n
100 = 5n
100/5 = n
20 = n
Resposta: n = 20
Questão 14
1-) Calculamos a quantidade de números, entre 100 e 500, que são divisíveis por 8.
Dados: P.A.(104,...,496); a1 = 104 ; an = 496 ; r = 8 ; n = ?
Resolução:
an = a1 + (n-1).r
496 = 104 + (n-1).8
496 = 104 + 8n - 8
496 = 96 + 8n
496 - 96 = 8n
400 = 8n
400/8 = n
50 = n
2-) Calculamos a quantidade de todos os números, entre 100 e 500.
Dados: P.A.(100,...,500); a1 = 100 ; an = 500 ; r = 1 ; n = ?
Resolução:
an = a1 + (n-1).r
500 = 100 + (n-1).1
500 = 100 + n - 1
500 = 99 + n
500 - 99 = n
401 = n
3-) Calculamos o número de termos que não são divisíveis por 8, fazendo: n = 401 - 50 = 351
Resposta: n = 351
Questão 15
P.A.(1, _, _, _, _, _, _, _, _, _, _, _,37)
Dados: a1 = 1 ; r = ? ; an = a13 = 37 ; n = 13
Resolução:
an = a1 + (n-1).r
a13 = 1 + (13-1).r
37 = 1 + 12.r
37 -1 = 12r
36 = 12r
36/12 = r
3 = r
Calculamos as 11 interpolações:
a2 = a1 + r = 1+3 = 4
a3 = a2 + r = 4+3 = 7
a4 = a3 + r = 7+3 = 10
a5 = a4 + r = 10+3 = 13
a6 = a5 + r = 13+3 = 16
a7 = a6 + r = 16+3 = 19
a8 = a7 + r = 19+3 = 22
a9 = a8 + r = 22+3 = 25
a10 = a9 + r = 25+3 = 28
a11 = a10 + r = 28+3 = 31
a12 = a11 + r = 31+3 = 34
Resposta: P.A.(1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37)
Questão 16
Dados: P.A.(2,...,66); a1 = 2 ; an = 66 ; r = 8 ; n = ?
Resolução:
an = a1 + (n-1).r
66 = 2 + (n-1).8
66 = 2 + 8n - 8
66 = 8n - 6
66 + 6 = 8n
72 = 8n
72/8 = n
9 = n
Subtraímos 2 termos dos 9 termos encontrados: n = 9 - 2 = 7.
Resposta: n = 7
Questão 17
Dados: P.A.(10, _, _, _, _, _, _,500); a1 = 10 ; an = a8 = 500 ; r = ? ; n = 8
Resolução:
an = a1 + (n-1).r
500 = 10 + (8-1).r
500 = 10 + 7.r
500 - 10 = 7r
490 = 7r
490/7 = r
70 = r
Calculamos as 6 interpolações:
a2 = a1 + r = 10+70 = 80
a3 = a2 + r = 80+70 = 150
a4 = a3 + r = 150+70 = 220
a5 = a4 + r = 220+70 = 290
a6 = a5 + r = 290+70 = 360
a7 = a6 + r = 360+70 = 430
Calculamos a média aritmética:
M.A. = Adição dos termos / número de termos adicionados = (a2 + a3 + a4 + a5 + a6 + a7) / 6
M.A. = (80 + 150 + 220 + 290 + 360 + 430) / 6 = 1530 / 6 = 255
Resposta: M.A. = 255
Questão 18
P.A.(3,..,88)
Dados: a1 = 3 ; r = ? ; an = a18 = 88 ; n = 18
Resolução:
an = a1 + (n-1).r
a18 = 3 + (18-1).r
88 = 3 + 17.r
88 - 3 = 17r
85 = 17r
85/17 = r
5 = r
Calculamos as 16 interpolações:
a2= a1 + r = 3+5 = 8
a3= a2 + r = 8+5 = 13
a4= a3 + r = 13+5 = 18
a5= a4 + r = 18+5 = 23
a6= a5 + r = 23+5 = 28
a7= a6 + r = 28+5 = 33
a8= a7 + r = 33+5 = 38
a9= a8 + r = 38+5 = 43
a10= a9+ r = 43+5 = 48
a11= a10+ r = 48+5 = 53
a12= a11+ r = 53+5 = 58
a13= a12+ r = 58+5 = 63
a14= a13+ r = 63+5 = 68
a15= a14+ r = 63+5 = 73
a16= a15+ r = 73+5 = 78
a17= a16+ r = 78+5 = 83
Resposta: Marcos quilométricos: 8, 13, 18, 23, 28, 33, 38, 43, 48, 53, 58, 63, 68, 73, 78, 83
Questão 19
Dados:
M(5) = 1000, 1005, ..., 9995, 10000.
M(7) = 1001, 1008, ..., 9996.
M(35) = 1015, 1050, ... , 9975.
M(1) = 1, 2, ..., 10000.
Resolução:
Para múltiplos de 5, temos: an = a1+ (n-1).r => 10000 = 1000 + (n - 1). 5 => n = 9005 / 5 => n = 1801.
Para múltiplos de 7, temos: an = a1+ (n-1).r => 9996 = 1001 + (n - 1). 7 => n = 9002 / 7 => n = 1286.
Para múltiplos de 35, temos: an = a1 + (n - 1).r => 9975 = 1015 + (n - 1).35 => n = 8995 / 35 => n = 257.
Para múltiplos de 1, temos: an = a1 + (n -1).r => 10000 = 1000 + (n - 1).1 => n = 9001.
Sabemos que os múltiplos de 35 são múltiplos comuns de 5 e 7, isto é, eles aparecem no conjunto dos múltiplos de 5 e no conjunto dos múltiplos de 7 (daí adicionarmos uma vez tal conjunto de múltiplos).
Total = M(1) - M(5) - M(7) + M(35).
Total = 9001 - 1801 - 1286 + 257 = 6171
Resposta: n = 6171
Questão 20
P.A.(6530, _ , 23330)
Dados: a1 = 6530 ; r = ? ; an = 23330 ; n = 3
Resolução:
an = a1 + (n-1).r
a3 = 6530 + (3-1).r
23330 = 6530 + 2.r
23330 - 6530 = 2r
16800 = 2r
16800/2 = r
8400 = r
a2 = a1 + r
a2 = 6530 + 8400
a2 = 14930
P.A.(6530, 14930, 23330, _ , _, _)
Dados:
a1 = 6530 ; r = 8400 ; an = a6 = ? ; n = 6
Resolução:
an = a1 + (n-1).r
a6 = 6530 + (6-1).8400
a6 = 6530 + 5.8400
a6 = 6530 + 42000
a6 = 48530
Resposta: a) 14930; b) 48530
----------------------------------------------------------------------------------------------------
PROGRESSÃO GEOMÉTRICA - P.G.
Definição
É uma sequência em que cada termo, a partir do segundo, é o produto do anterior com uma constante, denominada razão, representada pela letra 'q'.
Elementos
a1 : 1o termo
an : termo genérico, termo geral (ou n-ésimo termo)
q : razão
n : número de termos
Sn : soma dos termos
Pn : produto dos termos
Fórmula do Termo Geral da P.G.
an = a1 . qn-1
Produtos dos Termos de uma P.G.
O produto dos 'n' termos de uma P.G. é dado por:
ou
P.G. limitada (ou finita)
Obs.: para -1 < q < 1 e o número de termos tendendo ao infinito.
Termo Médio de uma P.G.
TM2 = a1.an
Representação de 3 termos na P.G.
Para representar três termos em P.G., sendo dado o produto dos termos, use:
Exercícios - Progressão Geométrica - P.G.
Questões de P.G
1-) Escreva os cinco primeiros termos de cada P.G., sendo dados:
a) a1 = 2 e q = 3
Resposta: P.G. (2, 6, 18, 54, 162, ...)
b) a1 = 3 e q = -1
Resposta: P.G. (3, -3, 3, -3, 3, ...)
c) a1 = -6 e q = 1/2
Resposta: P.G. (-6; -3; -1,5; -0,75; -0,375; ...) ou (-6; -3; -3/2; -3/4; -3/8; ...)
d) a1 = -2 e q = 5/4
Resposta: P.G. (-2; -5/2; -25/8; -125/32; -625/128; ...)
e) a1 = 7 e q = 0
Resposta: P.G. (7, 0, 0, 0, 0, 0, ...)
f) a1 = q = 1
Resposta: P.G. (1, 1, 1, 1, 1, ...)
2-) Calcule o valor do primeiro termo de uma P.G., sabendo que o quarto termo é -108 e a razão é q = 3.
3-) A soma do 2º com o 3º termo de uma P.G. vale 16 e o produto do 1º com o 3º é 16. Determine essa P.G. sabendo que ela é crescente.
Resolução:
a2 + a3 = 16 (I)
a1 . a3 = 16 (II)
Fazer a3 = a1 . q2 e substituir em (II).
a1 . a1 . q2 = 16
a12 . q2 = 42
Extrair a raiz quadrada dos dois membros.
a1 . q = 4
a1 = 4/q
Se a2 = a1 .q
a2 = 4/q . q
a2 = 4
Como a2 + a3 = 16, temos:
a3 = 12
q = a3 / a2 = 12/4 = 3
Daí a1 = 4/q
a1 = 4/3
Resposta: P.G. (4/3, 4, 12, ...)
4-) Interpole quatro meios geométricos entre 1/8 e 4.
5-) Interpole seis meios geométricos entre 1 e 2187.
Resolução:
an = a1. qn-1
2187 = 1 . q8-1
2187 = 1 . q7
Fatorando 2187, temos: 2187 = 37.
Então, 37 = q7
Se os expoentes são iguais, as bases das potências também são iguais. Logo, q = 3
a2 = a1 . q
a3 = a2 . q
a4 = a3 . q
a5 = a4 . q
a6 = a5 . q
a7 = a6 . q
P.G.(1, 3, 9, 27, 81, 243, 729, 2187)
6-) Uma pessoa aplicou R$ 8.000,00 à taxa de 2,5 por cento ao mês. Calcule por quanto tempo esse dinheiro deve ficar aplicado para que o montante seja de R$ 11.586,38. (Use log 1,025 = 0,0107 e log 1,4129732 = 0,1501.)
7-) Calcule a soma dos 6 primeiros termos da P.G. (7, 14, ...).
Resolução:
Sn = a1. (qn - 1) / q - 1
S6 = 7 . (26 - 1) / 2 - 1
S6 = 7 . (64 - 1) / 1
S6 = 7 . 63
S6 = 441
Webmaster: Adriano Sumar Cardoso
Teacher of Mathematic / Professor de Matemática
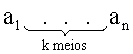









Nenhum comentário:
Postar um comentário